Big-O Notation | Algorithms | DroidTechKnow

In Computer Science, Big-O is a standard mathematical notation that is used to measure the efficiency of an algorithm relative to its input size in the worst-case scenario. In other words, Big-O notation is a language that we used to measure the time or space complexity of an algorithm. To measure the efficiency of an algorithm, we need to measure the two things.

• Time complexity:How much time is needed to run an algorithm.

• Space Complexity:How much space is needed to run an algorithm.

Big-O notation represents the upper bound of running algorithms relative to the input size. As it represents the upper bound so it will always give you the worst-case complexity of an algorithm. It is represented as:

f(n) = O(inputSize)

How to calculate the Complexity

You need to follow below 3 steps to calculate the complexity of any program.

1. Write down each step with their execution count

2. Make an equation by summing all the step count in terms of n.

We are taking an example to understand more.

function example() { 
  var sum = 0;
  for(var a=0; a<10; a++) {  
    sum = sum + a;
  } 
  console.log(sum);
}

Step 1: List all the steps with their count.

Operations / Steps	Num of Executions
var sum = 0	1
for (int a=0;a<10;a++)	11
sum = sum+a	10
console.log(sum);	1

Step 2: Sum all the steps

=> 1 + 11 + 10 + 1

Now generalize the above equation in terms of n (input size).

=> 1 + (n + 1) + n + 1

=> 3 + 2n

Now remove contents and ignore lower order terms to get the Big-O Notation.

=> n =>O(n)

Examples of Big-O Notation

1. Constant Time O(1): O(1) describes the complexity of the function which always executes a single time irrespective of input data set.

function constant(n) {
  console.log('O1');
}

2. Linear Time O(N):O(N) describes the complexity of the function which always executes n number of times where n is the number of elements in the array. If the number of elements in the array grows then the time will also grow linearly. If the value of n is 10 then the function will prints “On” 10 times.

function linear(n) {
  for(var a=0; a<n; a++) {
   console.log('On');
  }
}

3. Quadratic Time O(N²):O(N²) describes the complexity of the function which always executes (n*n) number of times where n is the number of elements in the array. If the number of elements in the array grows then the time will also grow quadratically.If the value of n is 10 then the function will prints “On” 100 times.

function quadratic(n) {
  for(var a=0; a<10; a++) {
    for(var a=0; a<10; a++) {  
      console.log('On2'); 
    }
  }
}

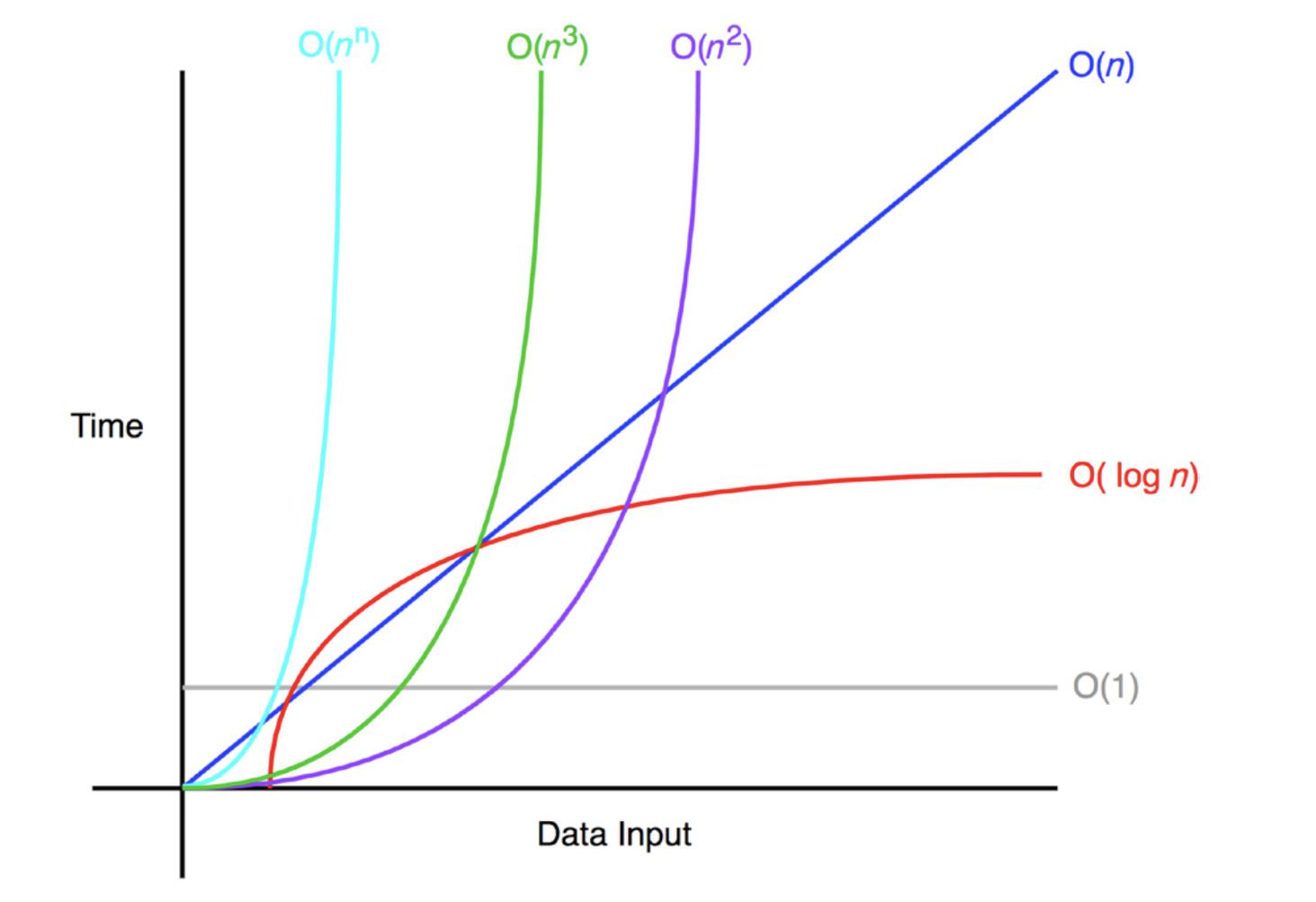
Below is a rough graph of different functions to visualize their Big-o notation.

Rules of Big-O notation

We will understand the rules of Big-O notation by taking an example. Suppose we have an algorithm complexity as f(n) where n represents the number of inputs, f(n)_time represents time complexing and f(n)_space represents the space complexity.

Coefficient Rule: “Get Rid ofConstants”

According to this rule, we canignore any non-input-size-related constants. All the coefficients will be ignored for the large input value. So the Big-O notation of f(n) and kf(n) will be the same for any constant k > 0.

Sum Rule: “Add Big-Os Up”

The Sum rule rules stated that, If some algorithm(A) depends on two other algorithms (B+C) then the Big-O notation of algorithm (A) should be the sum of Big-O notation of Algorithm B and C.

If f(n) is O(h(n)) and g(n) is O(p(n)), then f(n)+g(n) is O(h(n)+p(n)).

Product Rule: “Multiply Big-Os”

Similar to Sum Rule, Product rule stated that Big-O notation is multiplied if the time complexity of algorithms is multiplied.

If f(n) is O(h(n)) and g(n) is O(p(n)), then f(n)g(n) is O(h(n)p(n)).

Polynomial Rule: “Big-O tothePower ofk”

The polynomial rule stated that the Big-O notation of polynomial time complexity has the same degree that of the polynomial.

If f(n) is a polynomial of degree k, then f(n) is O(n^k).

Log of a power rule:

Similar to coefficients rule, constants within the log function also ignored in Big-O notation.

log(nk) is O(log(n)) for any constant k > 0.

Transitive rule:

If f(n) is O(g(n)) and g(n) is O(h(n)), then f(n) is O(h(n)).